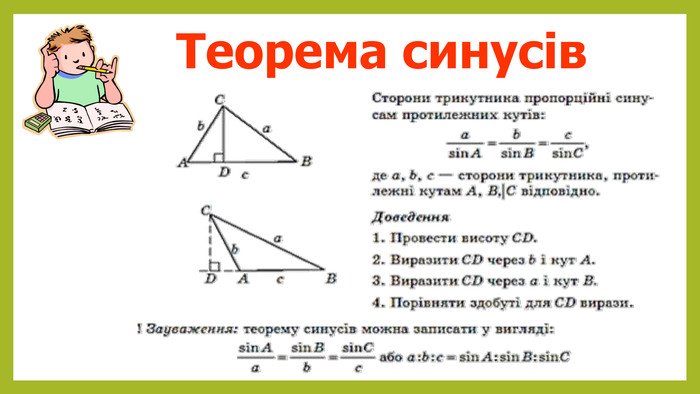
У тригонометрії теорема синусів є одним із ключових інструментів для розв’язання трикутників. Вона дозволяє знаходити невідомі сторони або кути в довільному трикутнику, використовуючи відношення сторін до синусів протилежних кутів. Це надзвичайно корисно як для учнів шкіл, так і для студентів, які вивчають математику, фізику або інженерію.
Профіль біографії: Теорема синусів
| Поле | Деталі |
| Назва | Теорема синусів |
| Галузь | Тригонометрія, геометрія |
| Застосування | Розв’язання довільних трикутників |
| Формула | a/sin A = b/sin B = c/sin C |
| Вперше застосована | Давньогрецькі та ісламські математики (III–X ст. н.е.) |
| Сфери використання | Математика, фізика, астрономія, інженерія |
| Рівень складності | Середній, рекомендовано для старшої школи |
Що таке теорема синусів?
Теорема синусів — це твердження, що в будь-якому трикутнику відношення сторони до синуса протилежного кута є однаковим для всіх трьох сторін і кутів:
a / sin A = b / sin B = c / sin C
Ця формула дозволяє обчислювати відсутні кути або сторони, якщо відомо достатню кількість інших величин.
Як виводиться формула теореми синусів?

Формула виводиться з геометрії кола, описаного навколо трикутника. Якщо в трикутнику ABC вписане коло, радіус якого R, то сторони трикутника пов’язані з синусами кутів так:
a / sin A = b / sin B = c / sin C = 2R
Звідси й виникає головне рівняння теореми синусів.
Коли застосовується теорема синусів?
Її доцільно використовувати у випадках:
- Відомі дві сторони і не включений між ними кут (SSA);
- Відомий один кут і дві прилеглі сторони (AAS або ASA);
- Відомі дві сторони та протилежний кут.
Завдяки цьому теорема особливо корисна в задачах на побудову або обчислення.
Приклад використання теореми синусів
Розглянемо трикутник ABC, де:
- ∠A = 40°, ∠B = 60°
- Сторона a = 10 см
Щоб знайти сторону b, використовуємо:
a / sin A = b / sin B
Підставляємо:
10 / sin(40°) = b / sin(60°)
Звідси:
b = 10 × sin(60°) / sin(40°) ≈ 10 × 0.866 / 0.642 ≈ 13.49 см
Отже, сторона b ≈ 13.5 см
У чому різниця між теоремою синусів і теоремою косинусів?
Теорема синусів застосовується тоді, коли відомі кути, а теорема косинусів — коли є дві сторони та кут між ними. Тобто:
- Теорема синусів — зручна для обчислення у «відкритих» трикутниках.
- Теорема косинусів — працює краще для «закритих» конфігурацій.
Геометричне значення: зв’язок із описаним колом
Цікаво, що через будь-який трикутник можна описати коло. Теорема синусів прямо пов’язує сторони трикутника з радіусом описаного кола:
a / sin A = 2R
Це означає, що сторони можна вимірювати не лише через кути, але й через радіус кола, що проходить через усі три вершини.
Помилки при використанні теореми синусів
Поширені помилки:
- Забування переводити кути в градуси або радіани (залежно від калькулятора);
- Використання неправильного кута в обчисленнях;
- Не перевірка, чи можливе існування трикутника при даних значеннях (умова існування трикутника).
Теорема синусів у фізиці та інженерії
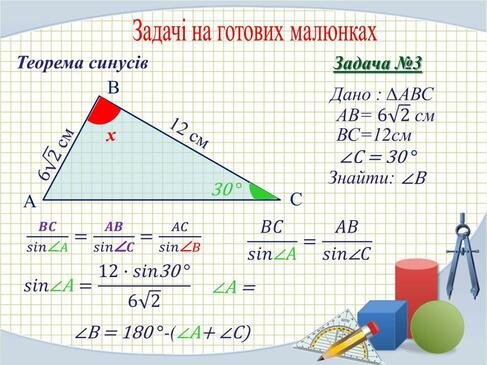
У фізиці вона часто застосовується в задачах на сили під кутами, а в інженерії — у визначенні довжин складних елементів конструкцій. Наприклад, при розрахунку нахилу даху, сили в балках або векторних розкладаннях.
Вивчення теореми синусів у школі
У шкільній програмі України теорема синусів входить до курсу 9 або 10 класу. Її включають у модулі з тригонометрії, і зазвичай супроводжують великою кількістю практичних задач.
Застосування в астрономії
Цікаво, що астрономи в давнину використовували тригонометрію для розрахунку відстаней до зірок. В основі багатьох методів лежить саме теорема синусів.
Практичні поради для запам’ятовування
- Усі відношення: сторона / sin кута напроти;
- Завжди перевіряйте одиниці виміру;
- Починайте з простих задач, поступово переходьте до складніших.
Висновок
Теорема синусів — це потужний інструмент, який варто добре засвоїти. Вона відкриває шлях до розв’язання багатьох задач у геометрії, фізиці, інженерії та навіть астрономії. Якщо ви навчитеся правильно застосовувати цю формулу, то зможете з легкістю вирішувати трикутники будь-якої складності.
Читати далі: Географія 7 клас – Повний огляд тем і порад для легкого навчання
Часті запитання (FAQ)
Це формула, яка дозволяє знайти невідомі сторони або кути в будь-якому трикутнику через синуси кутів.
Так, але зазвичай у прямокутних трикутниках зручніше використовувати синуси, косинуси й тангенси напряму.
У такому випадку теорему синусів не застосовують — краще використовувати теорему косинусів.
Так, якщо відомі дві сторони і кут між ними, площа дорівнює ½ ab sin C.
Вона дозволяє розв’язувати трикутники, які не є прямокутними, лише за допомогою одного кута і двох сторін.