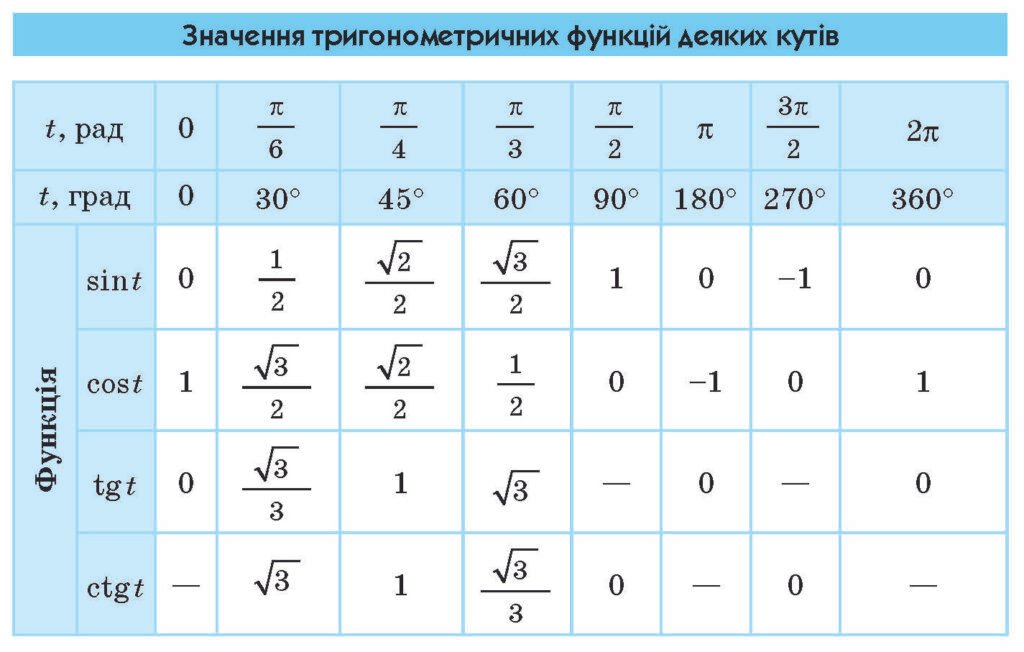
Тригонометрична таблиця — це основа вивчення тригонометрії у школі та університеті. Вона дозволяє швидко знаходити значення тригонометричних функцій таких як синус, косинус, тангенс та котангенс для основних кутів.
Що таке тригонометрична таблиця
Тригонометрична таблиця — це таблиця, в якій зазначені значення тригонометричних функцій для деяких стандартних кутів. Зазвичай у ній вказуються значення для кутів 0°, 30°, 45°, 60°, 90°, а також у радіанах: 0, π/6, π/4, π/3, π/2.
Ці значення часто використовуються у шкільній математиці, геометрії та фізиці. Саме тому варто їх вивчити або принаймні розуміти, як ними користуватись.
Навіщо потрібна тригонометрична таблиця
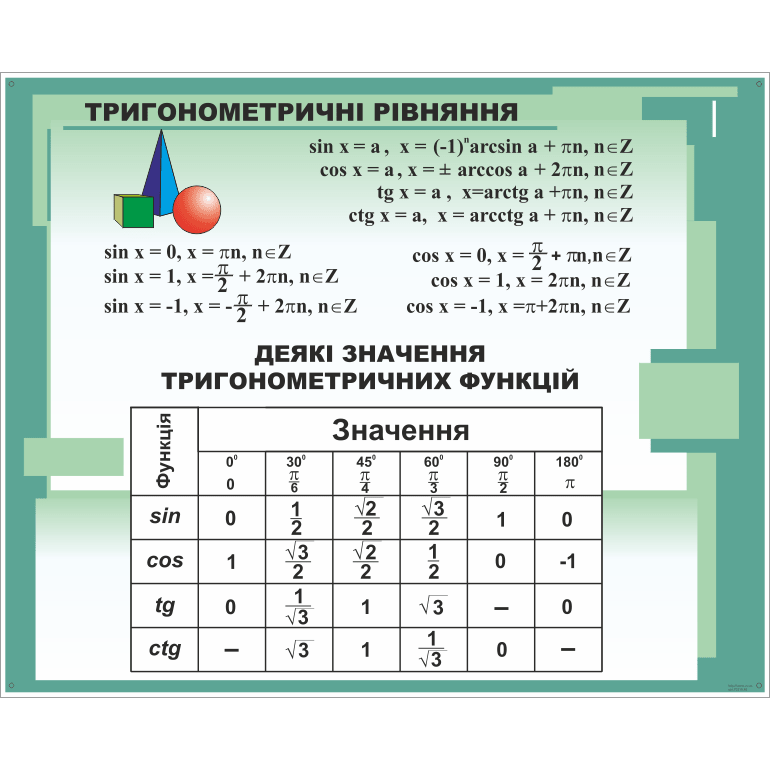
Важливо знати, що ця таблиця допомагає обчислювати сторони й кути у трикутниках. Крім того, її застосовують для:
- вирішення тригонометричних рівнянь;
- побудови графіків;
- обчислення векторів;
- прикладних задач у фізиці;
- навігації та астрономії.
Тригонометрична таблиця є незамінним інструментом у науці.
Тригонометрична таблиця: повна версія
| Кут | sin | cos | tg | ctg |
| 0° | 0 | 1 | 0 | — |
| 30° | 1/2 | √3/2 | √3/3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | √3/3 |
| 90° | 1 | 0 | — | 0 |
Знак “—” означає, що значення не визначено (наприклад, tg(90°) не існує, бо ділення на 0 неможливе).
Як запам’ятати тригонометричну таблицю
Є кілька простих способів запам’ятовування значень:
1. За допомогою пальців
Це відома «методика пальців»: розташовуємо руку долонею до себе. Кожен палець — це один із кутів (0°, 30°, 45°, 60°, 90°). Щоб знайти синус — рахуємо кількість пальців зліва від згинаного і ділимо на 2, а потім витягуємо квадратний корінь. Для косинуса — пальці праворуч. Формула:
sin(кут) = √(кількість пальців зліва) / 2
cos(кут) = √(пальці праворуч) / 2
2. За допомогою таблиці квадратів
Варто пам’ятати, що значення синуса і косинуса можна подати як √0/2, √1/2, √2/2, √3/2, √4/2 для кутів 0°, 30°, 45°, 60°, 90°. Просто розташовуємо їх по зростанню (для синуса) і навпаки (для косинуса).
Важливі формули з тригонометричної таблиці
Щоб краще користуватись таблицею, слід пам’ятати кілька ключових формул:
Синус і косинус сум і різниць:
- sin(α ± β) = sinα·cosβ ± cosα·sinβ
- cos(α ± β) = cosα·cosβ ∓ sinα·sinβ
Ці формули дозволяють знаходити значення тригонометричних функцій навіть для нестандартних кутів.
Тригонометрична таблиця в радіанах
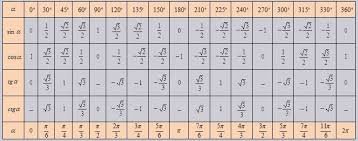
У старших класах і в університеті кути часто вимірюють у радіанах:
| Кут (радіани) | sin | cos | tg | ctg |
| 0 | 0 | 1 | 0 | — |
| π/6 | 1/2 | √3/2 | √3/3 | √3 |
| π/4 | √2/2 | √2/2 | 1 | 1 |
| π/3 | √3/2 | 1/2 | √3 | √3/3 |
| π/2 | 1 | 0 | — | 0 |
Практичні приклади використання
Тепер розглянемо, як можна використати тригонометричну таблицю в реальних задачах.
Приклад 1: Обчислення сторони трикутника
Є прямокутний трикутник із гострим кутом 30° і прилеглим катетом довжиною 10 см. Щоб знайти гіпотенузу, використаємо формулу:
cos(30°) = прилеглий катет / гіпотенуза
cos(30°) = √3/2
Розв’язавши рівняння:
√3/2 = 10 / x ⇒ x = 20/√3
Приклад 2: Визначення кута
Якщо ми знаємо, що sin(α) = 1/2, то з таблиці легко визначити:
α = 30°
Як будують тригонометричну таблицю
Значення в таблиці виводяться з одиничного кола. Це коло з радіусом 1, центр якого в початку координат. Точка на колі задається кутом, а її координати (x, y) — це cos і sin відповідного кута. Саме так будують таблицю.
Поради для учнів
- Завжди починайте з розуміння, а не зазубрювання.
- Малюйте схеми — це дуже допомагає!
- Використовуйте кольорові ручки для таблиць.
- Повторюйте значення щодня протягом тижня — пам’ять закріпиться.
- Створіть власну шпаргалку з тригонометричною таблицею.
Читати далі: теорема виета – Просте Пояснення для Школярів
Часті запитання (FAQ)
Тригонометрична таблиця — це набір значень синуса, косинуса, тангенса і котангенса для основних кутів, які часто використовуються в математиці.
Є метод “пальців”, а також спосіб через √0/2, √1/2, √2/2 і так далі. Вони прості й ефективні.
Тому що tg(α) = sin(α)/cos(α), а cos(90°) = 0. Ділення на нуль — неможливе.
У шкільній математиці, алгебрі, геометрії, фізиці, навігації, комп’ютерній графіці та навіть в архітектурі.
Так, але краще розуміти логіку побудови — так ви не забудете її надовго.
Висновок
Тригонометрична таблиця — це корисний інструмент, який значно полегшує роботу з кутами і сторонами в трикутниках. Її легко запам’ятати, якщо застосовувати прості методи. Також важливо не просто вивчити її, а зрозуміти, як вона працює. Це знання точно знадобиться вам і в школі, і далі у житті.